|
National Technical University of Athens School of Chemical Engineering Department of Materials Science and Engineering Computational Materials Science and Engineering Group (Co.M.S.E.) |
| News 30 June 2025 A PhD program with title "PhD Program in Process and Product Engineering" is available in the group of Profs. Giovanni Ianniruberto and Pino Marrucci at the Universita di Napoli. Click here for the more details. Click here for the more details. 12 June 2025 The European Materials Informatics Network (EUMINe) invites students/scientists in the field of materials science to participate in the upcoming EUMINe Training School which will take place on 19-20 June 2025 at the Alex Castella Hotel in Piraeus, Greece. Click here for the more details. 31 March 2025 We would like to invite you to our group's next meeting, which will take place next Tuesday, April 1st, at 14:00, in the "N. Koumoutsou" room of the School of Chemical Engineering, NTUA. Professor Theodoros Karakasidis, Chairman of the Department of Physics at the University of Thessaly, will discuss an extremely interesting and timely topic, namely the prediction of material properties using machine learning methods. Click here for the abstract of the presentation. 9 May 2024 A summer school/Workshop is organized by the Department of Mathematics of the University of the Aegean, in cooperation with the Hellenic Society of Rheology (HSR). Τhe event is open to all M.Sc. and Ph.D. students, post-docs, scientists and engineers conducting research or interested in the field of rheology and fluid mechanics. The program will consist of 6 short courses, invited lectures, a poster session and a limited number of oral presentations. All topics in theoretical, computational, and experimental rheology are welcome. Click here for more information. 28 March 2024 The Chemical Engineering department of the Technical University of Denmark (DTU) is seeking a motivated PhD student who is willing to be part of a world-leading research environment and contribute to the development of thermodynamic models and algorithms for electrolyte solutions. The appointment of this PhD position will be at the Center for Energy Resources Engineering (CERE), Department of Chemical and Biochemical Engineering. Click here for more information. PhD and Postdoctoral opportunities in Applied Knot Theory at ASU. Click here for more information. 6 December 2023 PhD and Postdoctoral opportunities in Applied Knot Theory at ASU. Click here for more information. 20 November 2023 Two PhD positions are available within the framework of the European Network "ReBond". Click here and here for more information. 19 September 2023 PhD position available in Computational Chemistry/Polymers Degradation funded by PlasticUnderground Marie Curie ITN. Click here for more information. 2 September 2023 Masters, PhD, Postdoctoral and Project-Manager positions are available at FORTH-IESL in the field of Synthesis, Experiments and Modelling/Simulations of Soft Matter systems (with emphasis in Polymers and Colloids) for Green and sustainable applications. Click here for more information. 2 September 2023 A PhD position on molecular-dynamics simulations of thermomechanical behaviour of epoxy-copper interfaces is available starting from January 2024 in the Soft Matter and Biological Physics (SMB) group of the Applied Physics department of TU/e. The project will be supervised by prof. dr. Alexey Lyulin. Click here for more information. 12 June 2023 On Friday, the 7th of July, 2023, two distinguished professors from the USA will visit the Computational Materials Science and Engineering (CoMSE) group at NTUA: Professor Bradley Chmelka (Department of Chemical Engineering, University of California, Santa Barbara) and Professor Eleni Panagiotou (School of Mathematical and Statistical Sciences, Arizona State University). In the context of their visit they will give lectures on their research work, with the following titles: Prof. Bradley Chmelka; Compositional and structural order at inorganic-organic interfaces. Prof. Eleni Panagiotou; Novel topological metrics of entanglement in polymers. The lectures will be given in the Koumoutsos room of the School of Chemical Engineering at NTU Athens, starting at 14:00. Click here for more information. 25 April 2023 The 2023 European Conference on Computational and Theoretical Chemistry, co-organized by the Greek Chemists Association and the Division of Computational and Theoretical Chemistry of the European Chemical Society will be held in Thessaloniki, 27-31 August 2023. Click here for more information. Read all news... |
Computational Materials Science and Engineering Group: Objectives The Computational Materials Science and Engineering (CoMSE) research group at the National Technical University of Athens was instituted in the summer of 2002 with the following objectives:
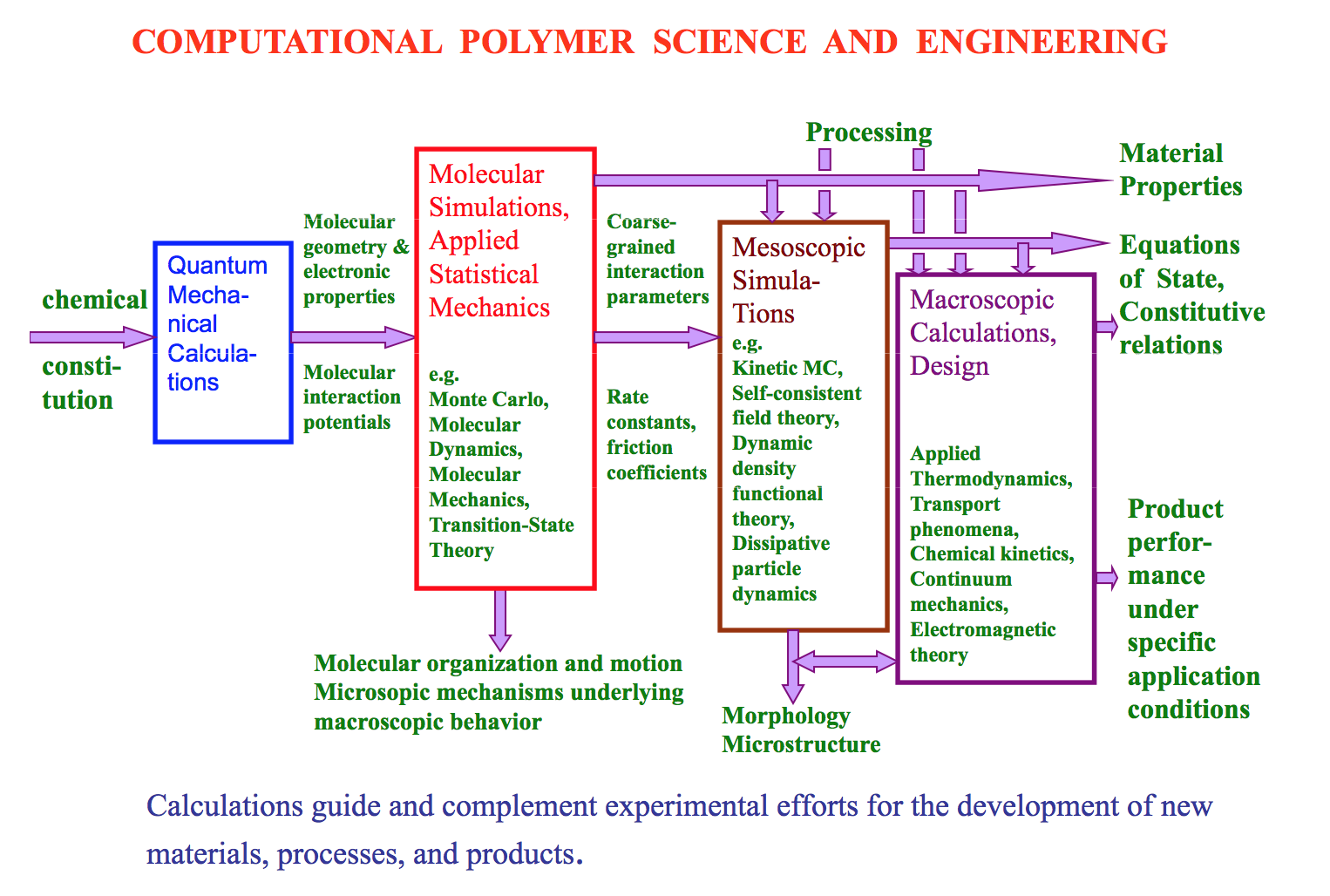
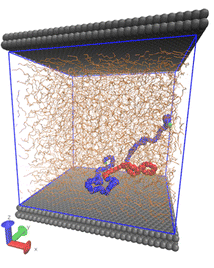
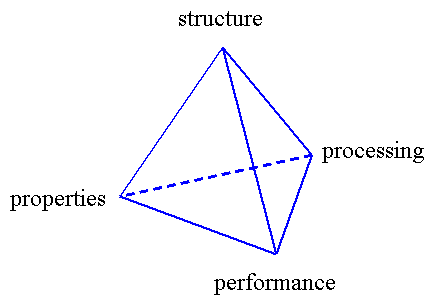 Materials Science and Engineering is often depicted as a tetrahedron having structure, properties, processing, and performance as its apices (S.A. Allen and E.L. Thomas, The Structure of Materials, Wiley: New York, 1998; p 2). Research at CoMSE aims at developing computational methods that can elucidate/predict the relationships symbolized by the tetrahedron. A major challenge faced by materials modellers is that structure and dynamics are characterized by extremely broad spectra of length and time scales. This is depicted schematically in the figure below for polymeric materials. By comparison, atomistic molecular dynamics simulations on the fastest computers available today can barely track the evolution of materials systems of length scale = 100 nm for times on the order of 100 ns. Clearly, a single modelling or simulation approach cannot address all properties of real-life materials. The development of hierachical, or multiscale modelling approaches is imperative. Such approaches consist of many levels, each level addressing phenomena over a specific window of length and time scales; links between different levels can be established through systematic 'coarse-graining' of the model used to represent the material. At the base of this hierarchy, powerful atomistic simulation algorithms are needed, which can efficiently sample the complex potential energy hypersurfaces of polymeric materials, ensuring equilibration over the relevant time and length scales. The figure below provides a rough picture of how multiscale modelling approaches to the prediction of material properties can be developed. Multiscale modelling/simulation efforts can guide and complement experimental efforts for materials characterization and new materials development; conversely, experimental measurements are essential for validating the modelling approach. Multiscale modelling can be practised strictly sequentially (separate simulations at different levels, passage of parameters or functional relations from one level to another) or in parallel (simultaneous modelling at different levels and self-consistent zooming in and out between levels). |
|
 |
 |
 |

| Computational Materials Science and Engineering Group Department of Materials Science and Engineering School of Chemical Engineering, National Technical University 9 Heroon Polytechniou Street, Zografou Campus, 15780, Athens, Greece Tel. +30 210 772 3216, Fax +30 210 772 3112 Webmaster: comse.chemeng.ntua@gmail.com |
Copyright © 2023 - All rights reserved |