 |
National Technical University of Athens School of Chemical Engineering Department of Materials Science and Engineering Computational Materials Science and Engineering Group (Co.M.S.E.) |
| News 9 May 2024 A summer school/Workshop is organized by the Department of Mathematics of the University of the Aegean, in cooperation with the Hellenic Society of Rheology (HSR). Τhe event is open to all M.Sc. and Ph.D. students, post-docs, scientists and engineers conducting research or interested in the field of rheology and fluid mechanics. The program will consist of 6 short courses, invited lectures, a poster session and a limited number of oral presentations. All topics in theoretical, computational, and experimental rheology are welcome. Click here for more information. 28 March 2024 The Chemical Engineering department of the Technical University of Denmark (DTU) is seeking a motivated PhD student who is willing to be part of a world-leading research environment and contribute to the development of thermodynamic models and algorithms for electrolyte solutions. The appointment of this PhD position will be at the Center for Energy Resources Engineering (CERE), Department of Chemical and Biochemical Engineering. Click here for more information. PhD and Postdoctoral opportunities in Applied Knot Theory at ASU. Click here for more information. 6 December 2023 PhD and Postdoctoral opportunities in Applied Knot Theory at ASU. Click here for more information. 20 November 2023 Two PhD positions are available within the framework of the European Network "ReBond". Click here and here for more information. 19 September 2023 PhD position available in Computational Chemistry/Polymers Degradation funded by PlasticUnderground Marie Curie ITN. Click here for more information. 2 September 2023 Masters, PhD, Postdoctoral and Project-Manager positions are available at FORTH-IESL in the field of Synthesis, Experiments and Modelling/Simulations of Soft Matter systems (with emphasis in Polymers and Colloids) for Green and sustainable applications. Click here for more information. 2 September 2023 A PhD position on molecular-dynamics simulations of thermomechanical behaviour of epoxy-copper interfaces is available starting from January 2024 in the Soft Matter and Biological Physics (SMB) group of the Applied Physics department of TU/e. The project will be supervised by prof. dr. Alexey Lyulin. Click here for more information. 12 June 2023 On Friday, the 7th of July, 2023, two distinguished professors from the USA will visit the Computational Materials Science and Engineering (CoMSE) group at NTUA: Professor Bradley Chmelka (Department of Chemical Engineering, University of California, Santa Barbara) and Professor Eleni Panagiotou (School of Mathematical and Statistical Sciences, Arizona State University). In the context of their visit they will give lectures on their research work, with the following titles: Prof. Bradley Chmelka; Compositional and structural order at inorganic-organic interfaces. Prof. Eleni Panagiotou; Novel topological metrics of entanglement in polymers. The lectures will be given in the Koumoutsos room of the School of Chemical Engineering at NTU Athens, starting at 14:00. Click here for more information. 25 April 2023 The 2023 European Conference on Computational and Theoretical Chemistry, co-organized by the Greek Chemists Association and the Division of Computational and Theoretical Chemistry of the European Chemical Society will be held in Thessaloniki, 27-31 August 2023. Click here for more information. 06 April 2023 Doctoral thesis presentation: On Monday, April 24, our PhD student, Mr. Constantinos Revelas, will defend his Doctoral thesis, entitled: "Development of Self-Consistent Field Theory Models for Predicting the Structure and Properties of Inhomogeneous Polymer Systems: Application in Nanocomposite Materials" in front of his seven-member examination committee. The defense will take place at the Koumoutsos room of the Chemical Engineering School at 13:00. Click here to read an extended summary of the PhD. 04 April 2023 Sincerest congratulations to our group leader, Prof. Doros Theodorou, on publishing his autobiography in the Journal of Physical Chemistry B. It is published as a special issue (Festschrift) on the occasion of his 65th birthday. The special issue was edited by Ed Maginn, Ioannis Economou, Randy Snurr, and Arup Chakraborty. Click here to see the cover page or here to access the complete virtual special issue. 03 April 2023 Sincerest congraluations to our PhD students, Mr. Georgios Mikaelian and Mr. Fotis Venetsanos, on winning a doctoral fellowship from the Hellenic Foundation of Research and Innovation (aka ELIDEK). Very well deserved! 24 March 2023 Multiple postdoc positions available at MIT in the research laboratory of Richard Braatz on the integrated continuous manufacturing of mRNA-based biotherapeutics. Click here to find more details on the position and submission process. Read all news... |
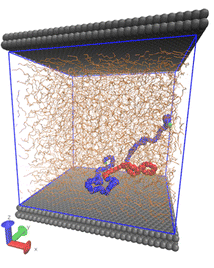
Polymer-matrix nanocomposites Polymer-matrix nanocomposites, i.e. nanoparticle-filled polymers, offer huge potential for future applications and energy savings, and are considered as an important branch of the emerging field of nanotechnology. The observation that, other things being equal, the effectiveness of the filler increases with an increase in surface to volume ratio has provided large impetus for a shift from micron- to nanosized filler particles. 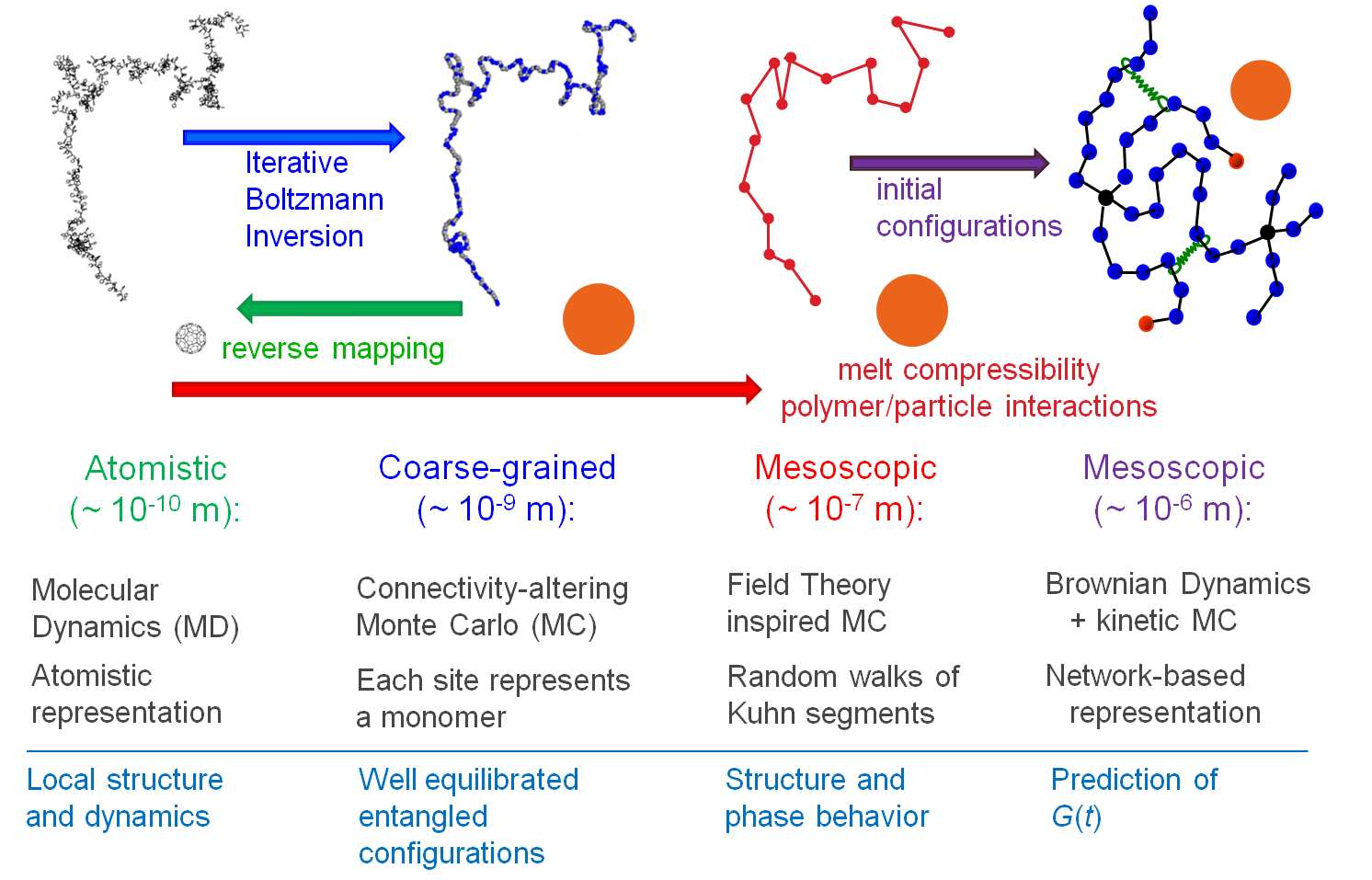 Figure 1: Levels of modeling developed for the study of polymer matrix nanocomposites, methods employed in each one and main simulation observables. Four interconnected levels of representation have been developed for polymer-matrix nanocomposites (Figure 1): (a) An atomistic one, where both nanoparticles and polymer chains are represented in terms of detailed atomistic force fields. Fullerenes (C60) are dispersed in PS matrix and atomistic Molecular Dynamics (MD) simulations are undertaken to uncover details of packing and to quantify (local and global) segmental dynamics and (atomic and local) stresses (Figure 2). 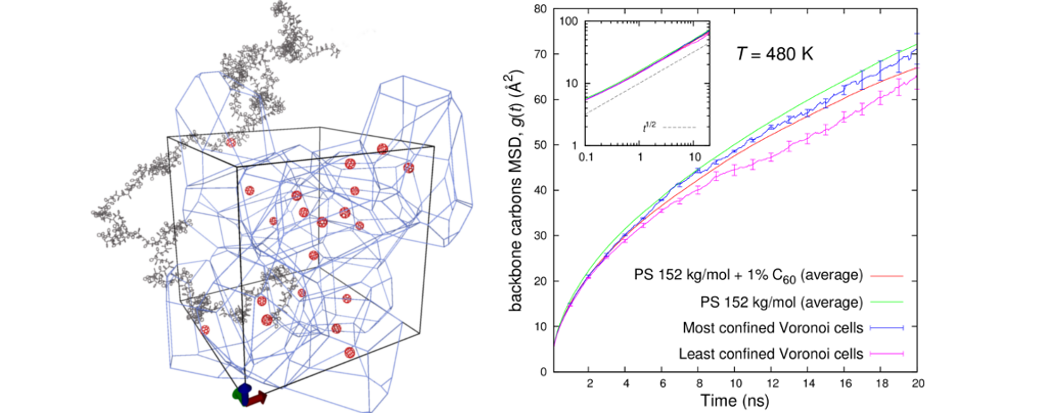 Figure 2: Quantification of many-particle influence on polymer dynamics via a Voronoi tessellation of the simulation box (left figure). Mean-square atomic displacements (MSD) of PS backbone carbon atoms as a function of time for pure PS and PS + 1% C60 (right-hand side figure). In the case of fullerene nanocomposites, an analysis of the dependence of backbone MSD on confinement is also presented for most and least confined Voronoi cells. External links: http://pubs.acs.org/doi/abs/10.1021/ma402214r, http://arxiv.org/abs/1401.4314 (b) A coarse-grained representation, in which each repeat unit is mapped onto a single "superatom", and each nanoparticle is viewed as a solid object interacting with the polymer superatoms and other nanoparticles via Hamaker-type potentials. Equilibration of coarse-grained polymer-nanoparticle systems at all length scales is achieved via connectivity-altering Monte Carlo (MC) moves. These simulations are important for generating well-equilibrated initial configurations for atomistic MD through reverse mapping. (c) A Field Theory-inspired Monte Carlo (FT-i MC) level, where polymer chains are represented as freely jointed sequences of Kuhn segments. For polymer-polymer interactions, an effective energy function is used, which prevents large departures of the local polymer density from its value in the bulk melt everywhere in the system. This simulation methodology is capable of capturing structural features at length scales on the order of hundreds of nanometers. Brush thickness and scattering curves from the grafted PS corona of silica particles dispersed in PS have been predicted (Figure 3). 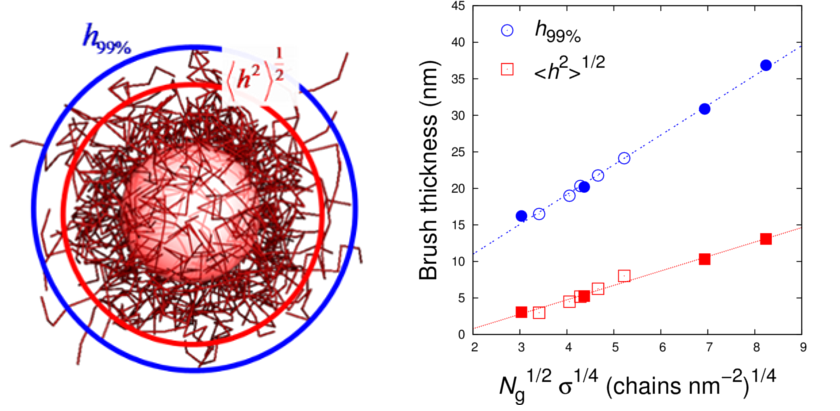 Figure 3: The calculated brush thickness (using two estimates indicated in the left figure) is plotted versus the square root of the degree of polymerization of grafted chains, Ng, times the fourth root of the grafting density, σ. Points correspond to systems containing an 8-nm-radius silica particle grafted with PS chains and dispersed in PS matrix. External links: http://pubs.acs.org/doi/abs/10.1021/ma400107q, http://arxiv.org/abs/1401.4001 (d) A slip-spring network representation where cross-links, entanglements and chain ends are the degrees of freedom of the polymeric matrix. From the thermodynamic point of view, the system under study is fully described by a Helmholtz energy function which accounts for the entropic springs connecting cross-links or entanglements, non-bonded interactions (derived from any appropriate equation of state, e.g. the Sanchez-Lacombe) and Hamaker interactions between nodal points - nanoparticles and nanoparticles - nanoparticles. Brownian simulations at this level, operating at the length scales of up to 1 μm and time scales up to 1 ms, account for changes in segmental mobility induced by the nanoparticles and track elementary events of chain slippage across entanglements, chain entanglement and re-entanglement. Relevant publications
Relevant projects
|
|
 |
 |
|
| Computational Materials Science and Engineering Group Department of Materials Science and Engineering School of Chemical Engineering, National Technical University 9 Heroon Polytechniou Street, Zografou Campus, 15780, Athens, Greece Tel. +30 210 772 3216, Fax +30 210 772 3112 Webmaster: comse.chemeng.ntua@gmail.com |
Copyright © 2023 - All rights reserved |